これはSimutrans Advent Calendar 2023 24日目の記事です。
ほかの記事もぜひご覧ください
昨年は身内NS用にインフラ系アドオンを作った話を書いたり、今年中も単発で線路アドオンの構成要素備忘録を書いたりしましたが、懲りずにその類の話です。半分くらい備忘録ですがよろしければご覧ください。
昔のアドオン、急坂にしか対応してなくない?
身内NSも2年半以上急坂環境だったので自分の古いアドオンも急坂にしか対応してないし、古いアドオンをリメイクするより新しいアドオンを作るほうが楽しいがために、自分のアドオンでも緩急坂に対応してないものも少なくないので人のこと言えないのですが、出来のいいアドオンが急坂しかなかったり、急坂から緩急坂環境に移行するときに急坂にしか対応していないと困りますよね。
2年位前までは急坂を使っていたので緩急坂対応のモダンなアドオンを急坂にすることはしょっちゅうやってたのですが、これは緩坂を無くすだけなのでdatを数行書き直せば(正規表現でも使って置き換えてしまえば)終わるので特段問題にはならないです。
逆はどうでしょう?急坂用アドオンに緩坂の画像は当然入っていないので作るか使えない前提で導入するしかないですが、さすがに緩坂無しは現実的ではないですよね。
なので、何とかして既存のソースから緩坂を作りたいですよね?というのが今回触れる内容です。
坂のタイルってどんな形?
こういうアドオンを作ったことがある人は復習程度に、あまり触れたことない人はふーん程度で流してみてください。
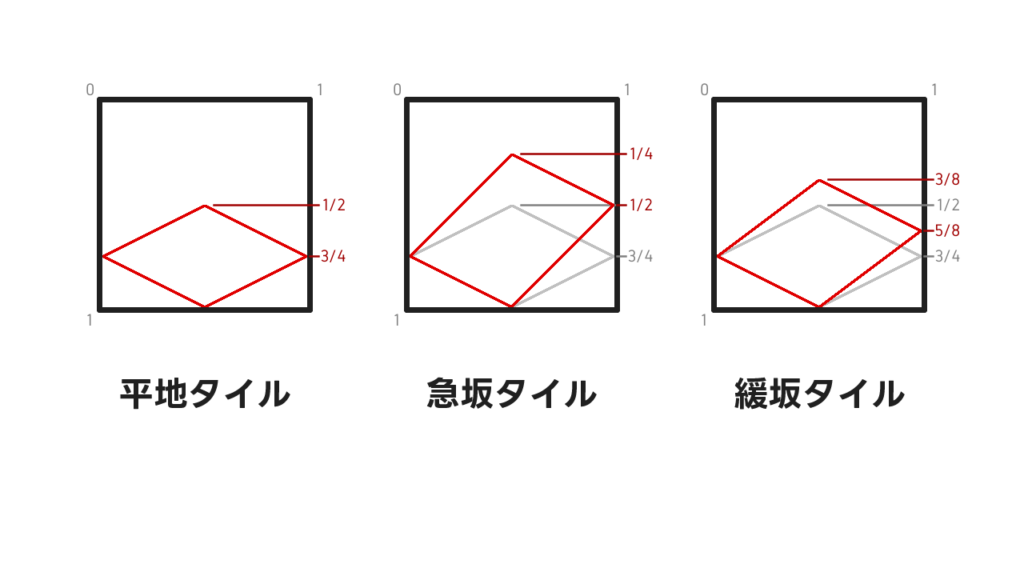
タイルの形を一般化してみた図です。タイル1枚の画像の大きさを0~1で表しましたが特定のパックセットのサイズにするにはそのままパックセットのサイズを掛けてもらえばよいです。
タイルはひし形なので普通に拡大縮小しようとすると坂の上と下の辺が変形してしまいます。そのまま変換が出来ないのですがどうしましょうか。
変形させてみる
前章ではタイルがひし形なために普通に拡大縮小がつかえない、という話でした。
なので、一般的な拡大縮小の操作が使えるようにするために坂の上と下の辺をそろえる変形を考えてみます。

まだ概念だけの説明ですがうまくいきそうな気がしてきました。
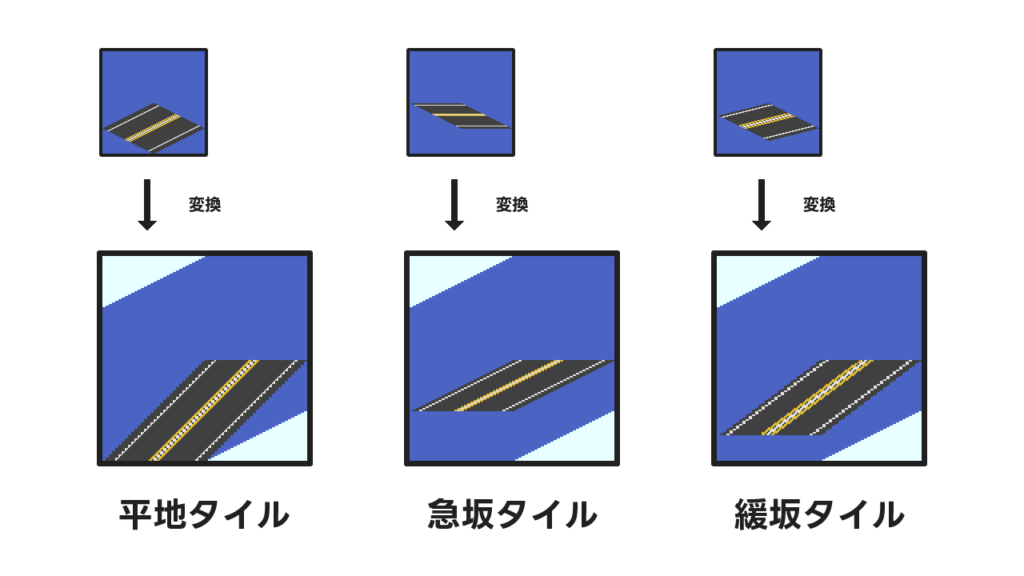
実際に3種類のタイルを変形してみましょう。
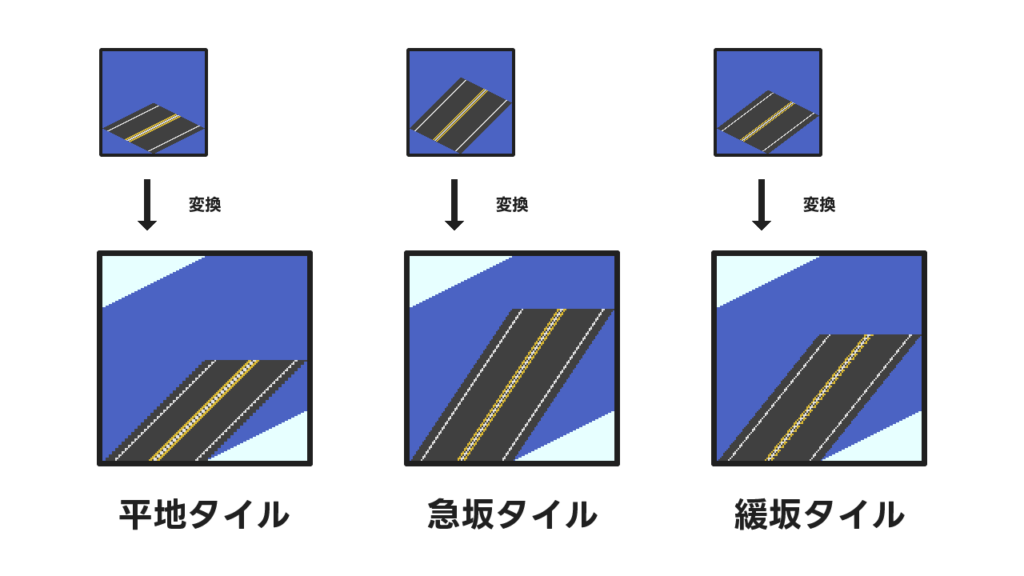
よさそうですね。この形にすれば普通の拡大縮小が使えるので、一つの画像からの変形でほかのタイルが生成できそうです。
試しに平地タイルと急坂タイルから緩坂タイル(平地タイルはついでに急坂タイルも)生成してみましょう。変形して拡大縮小を施し、先ほどとは逆の変換でタイルっぽく復元してみます。
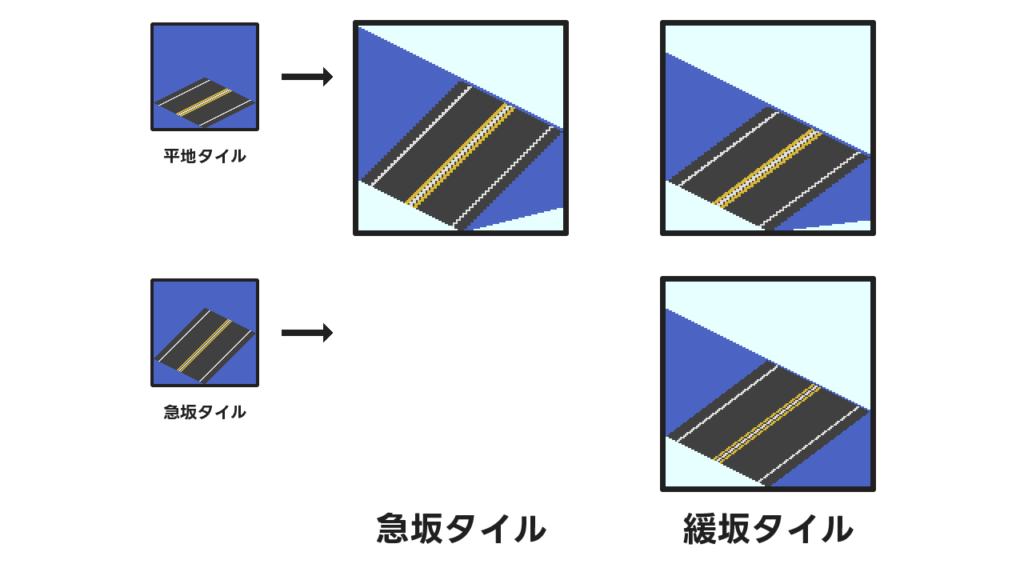
それっぽい形に変形できました!よかった!
でも同じ形なはずなのにずいぶん見た目がちがいますね。
拡大してみましょう
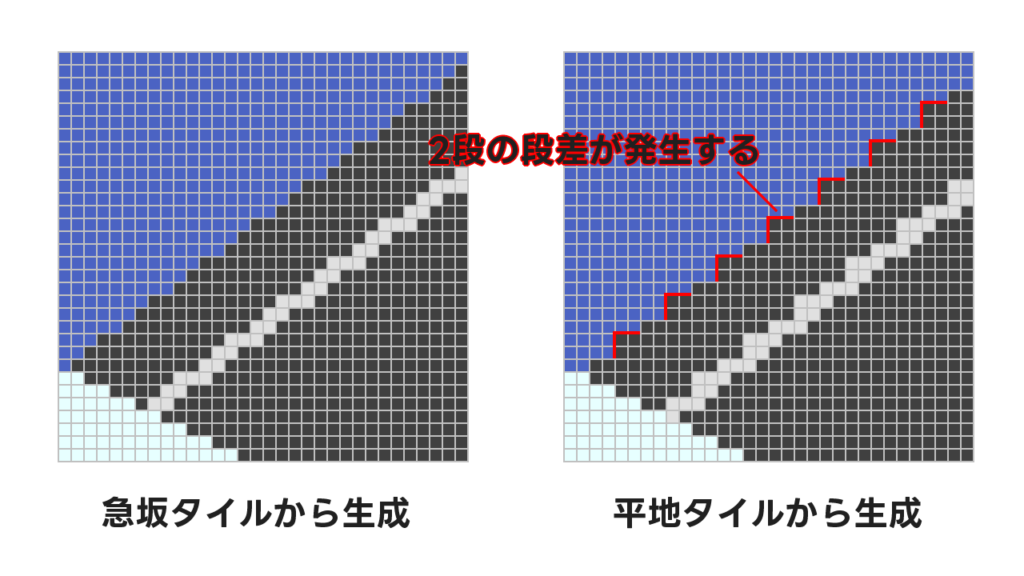
平地タイルから生成した画像は足りない箇所を複製で補っているため出来が良くないです。
急坂タイルから生成すると不要な箇所を減らす方向で画像を加工するためうまくいきやすいです。坂の上下のフチがうまく出ないときは縮小処理の時の端数処理をいじってあげるとよくなります。
奥に下がるタイルも変形させてみる
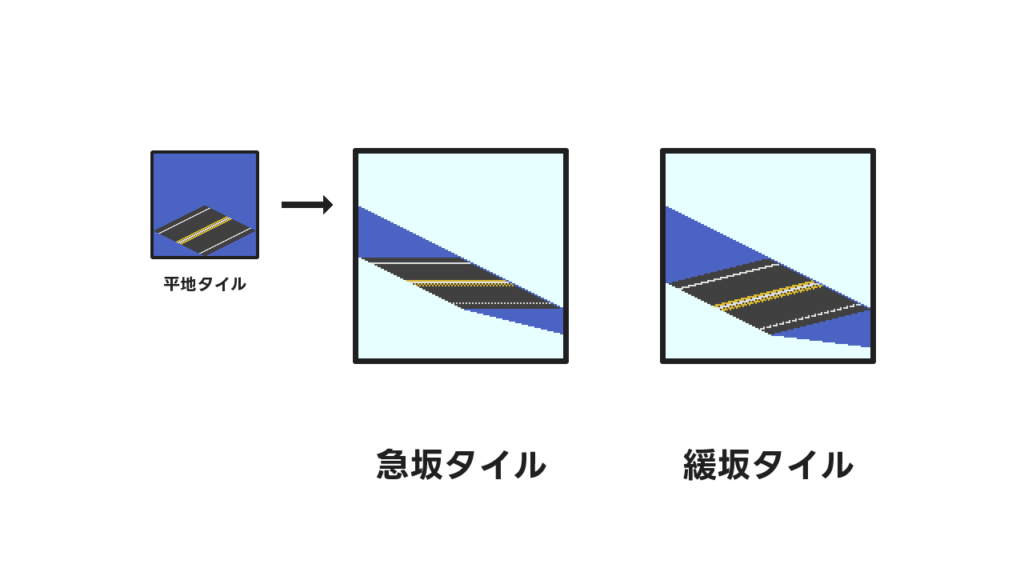
坂の下側がタイルの基準になっているので前章の変換後画像と揃っている場所が違いますがこちらも拡大縮小で作れそうですね。
平地タイルから縮小する形で変換してみます。
急坂の奥に下がるタイルは一直線にする都合上、ジャギーが出るとどうしようもないですが、緩坂のような線が斜めのタイルは変換前のタイルにアンチエイリアスを施してあると結構まともに見えるはずです。
急坂の奥に上がるタイルからは緩坂タイルが生成出来て、平地タイルから奥に下がるタイルが生成できましたね。
極論…?
急坂の奥に上がるタイルから緩坂タイルが生成できたので同じ要領で平地タイルも生成できます。そして平地タイルから各種手前から奥に下るタイルも作れました。
ということは急坂の奥に上がるタイルで各種タイルが、左右反転も利用すれば角や斜め以外のタイルが生成できそうです。
以下は実際にやってみた結果です。
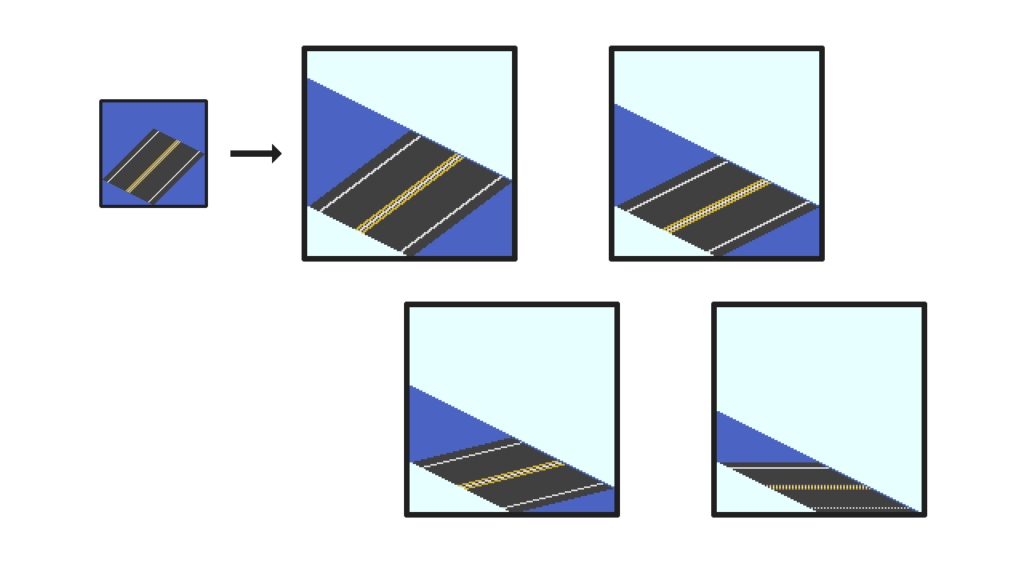
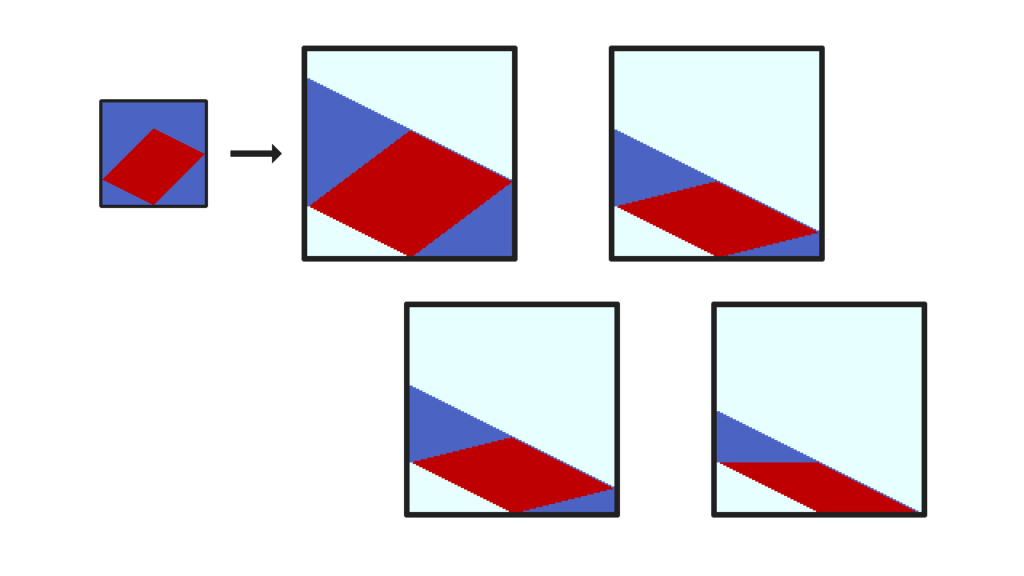
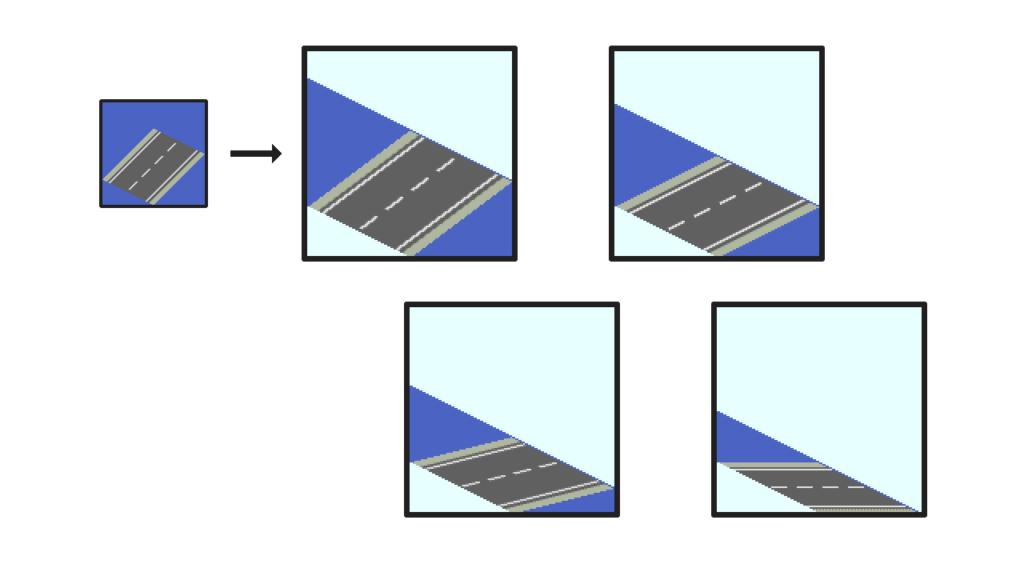
ざっくり変換してるのでフチがずれていたりしますが、おおむね上手く生成できそうです。アンチエイリアスつきの画像でやると違和感もほとんどないと思います。
まとめ
変換を駆使することで急坂の奥に上がるタイルから4種類のタイルができた。
なお3回の変形は線形変換をしているだけなのでこれと同じことを行列変形で行えばよい。
おまけ
pythonのOpenCV(CV2)とnumpyで行列変形をしてみたサンプルです。プログラムで扱うとY軸が上下反対になるのでプログラムと表記してる行列が異なります。
参考:Python, OpenCVで幾何変換(アフィン変換・射影変換など) | note.nkmk.me
αは拡大の割合で生成後/ソース画像の縦です
(HTMLにJS直打ちしたらWordPressの改行処理と競合するのか行列を1行に複数表示できなかったので2回目の変換までを合成した行列を置いておきます。合成前の行列は画像で確認してください) \begin{bmatrix} 1 & 0 \\ 0.5α & α \\ \end{bmatrix} 3回目は1回目と逆の変換を行いタイルの形状に復元します \begin{bmatrix} 1 & 0 \\ 0.5(1-α) & α \\ \end{bmatrix}
import cv2
import numpy as np
def show(img):
cv2.imshow("image",img)
cv2.waitKey(0)
img = cv2.imread("sidewalk.png")[:128,3*128:4*128] # 画像読み込み
size = (128, 128)
for last in [80,64,48,32]:
alpha = last/96
mat_1 = np.array(
[
[ 1, 0, 0],
[-0.5, 1, 0], # Y軸が上から下からなのでY軸を反転させている
],
dtype=np.float32
)
mat_2 = np.array(
[
[ 1, 0, 0],
[-0.5*alpha, alpha, 96-last],
],
dtype=np.float32
)
mat_3 = np.array(
[
[ 1, 0, 0],
[0.5*(1-alpha), alpha, 96-last], # Y軸が上から下からなのでY軸を反転させている、位置を合わせるためにY軸方向に平行移動
],
dtype=np.float32
)
cv2.imwrite("gyoretu"+str(last)+"_1.png",cv2.warpAffine(img,mat_1,size))
cv2.imwrite("gyoretu"+str(last)+"_2.png",cv2.warpAffine(img,mat_2,size))
cv2.imwrite("gyoretu"+str(last)+"_3.png",cv2.warpAffine(img,mat_3,size))

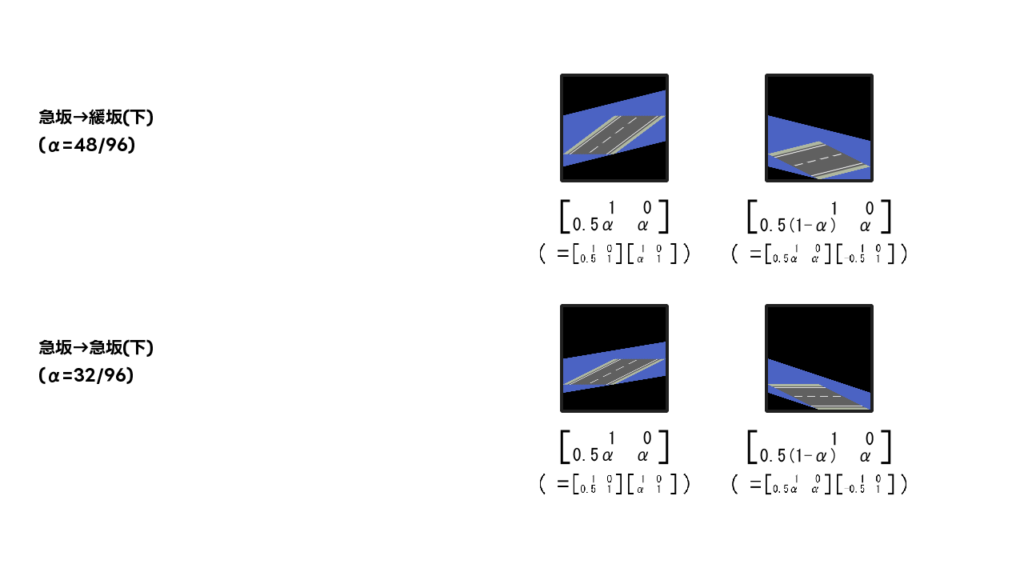
余談ですがこのために基礎だけかじりました
以下参考資料




コメント